课程「应用密码学与网络安全」期末复习笔记
本文是课程「应用密码学与网络安全」的2024年6月25日期末考前复习和实验报告的整合。
期末复习
引言
网络安全核心地位的关键目标是CIA3,即保密性、完整性、可用性、真实性和可追溯性。
OSI安全框架共包括安全攻击、服务和机制三个方面。安全攻击中分为被动和主动两种攻击;前者重点在于预防,后者可以被检测出来但很难有效防止。安全机制分为特定和普遍两种,应具备检测、防御或从安全攻击中恢复的能力——没有单一的机制可以提供所有安全服务。
传统加密技术
密码学是研究编制密码和破译密码的学科,因此分为编码学和分析学两个分支。本学科重点在于前者。
基于密码分析的攻击分为唯密文攻击、已知明文攻击、选择明文攻击、选择密文攻击和选择文本攻击五种。
绝对安全(也称无条件安全或信息论安全)的密码系统中敌手即使拥有无限的计算能力也能保障其安全性;其无法凭密文获取关于明文的任何信息。目前大多数公钥密码学原型能保证的是计算安全(即假设该公钥密码学方法在计算上安全)。
现在考虑以下几个传统加密方法。
Caesar加密
假设现在有明文,那么不妨将字母按照字母表顺序编号为。那么明文可以表示为此时利用Caesar密钥进行加密运算
得到若干密码组合而成的密文编码可以选择对其按照字母表中的顺序转换为各种字母,得到密文。随后解密时只要用
即可得到明文编码。之后在按照字母表顺序对照解码即可得到明文。
单表置换加密
先将字母顺序随意打乱,使每个明文字母映射到一个不同的随机密文字母。因此,理论上这种加密方式的密钥总数可以有种;这个值显然比要大得多。然而因为每个字母使用频率不同等人类语言自带的特性,这个加密方法看似安全其实在实际应用时也并不是那么的理想。
Playfair加密
吸取了单表置换加密中密钥空间小导致无法提供安全性的经验,Charles Wheatstone在1854年以其朋友Baron Playfair为名发明了一种多字母代替密码。其在一个五阶矩阵中首先填写密钥单词,之后将剩余(未出现在这个单词中的)字母拿来填写矩阵中尚未填入的空白中;当将I与J等效时,26个字母恰好能够放入这个总共25个格子的矩阵中。
现在思考以下实例。
以「monarchy」为密钥的Playfair加密。
首先先将密钥有序填入表格。
| M | O | N | A | R |
| C | H | Y | ||
此时剩下的字母还有“BDEFGIJKLPQSTUVWXZ”。将这些字母填入,得到密码表
| M | O | N | A | R |
| C | H | Y | B | D |
| E | F | G | I/J | K |
| L | P | Q | S | T |
| U | V | W | X | Z |
现在开始加密。以2个字母为一组进行加密;对于这个字母组可能会出现如下情况:
- 字母组的2个字母在这张表格中位于同行。假设这个字母组是“hd”,那么将这个字母组的两个字母分别向右移动一格,得到密文“YC”(如果明文已经在这一行的最右端则循环回最左端)。
- 字母组的2个字母在这张表格中位于同列。假设这个字母组是“pv”,那么将这个字母组的两个字母分别向下移动一格,得到密文“VO”(如果明文已经在这一列的底部则循环回顶部)。
- 其他情况。假设字母组是“SE”,那么将这两个字母作为对角线所构造出的矩形单独取出,寻找对应的另一条对角线,其两端按明文中两个字母所在行号出现的顺序进行排序得到“LI”或“LJ”。
解密的思路根据加密方法逆向完成即可。
Hill密码
由Lester Hill于1929年发明的多字母代替密码。其利用模运算意义下的矩阵乘法、矩阵求逆、线性空间等概念实现。
现在,考虑下方的例子。
使用下方所示的矩阵K对明文P=“mor”进行加密。
对上述密钥矩阵求逆,可以得到
而明文
(注意上方字母转编码是从开始编排的)因此密文
因此密文就是HDL。解密时只要用即可得到明文的矩阵。
多表置换密码
在明文消息中采用不同的单表置换,通过使各个字母的频率分布更平坦来提高安全性。
现在考虑下面两个例子。
(Vigenère密码)用密钥“MYKEY”加密明文“encode and decode”。
显然根据背景知道明文编码密钥编码因为明文长度大于密钥长度,所以将密钥通过重复循环延长至15位,即随后进行加密运算
转码得到密文“QLMSBQYXHBQAYHC”。解密时用等式即可得到明文的编码。
置换加密
通过某种置换改变明文字母的顺序来完成加密。一般采用的是一种“按波浪线顺序写出明文,以行的顺序写出密文”的栅栏技术;这种加密方式非常容易被破译。但是,通过多次置换后这个密码的安全性就会有非常大的提升。
现在考虑以下例子。
对明文“meet me after the toga party”依照置换加密方法进行1次加密。
将明文中的奇数位和偶数位分别拆开,得到
1 | m e m a t r h t g p r y 奇数位 |
因此经过一次置换加密得到的密文就是“MEMATRHTGPRYETEFETEOAAT”。
一次一密
随机生成每一次的密钥,理论上完全不可破解,但实际上也完全不可行。这是因为,产生大量的随机密钥是一件非常困难的事,这些密钥的分配和保护工作则让这个工作的难度进一步提高。
分组密码与DES
分组密码
将一个明文组作为整体进行加密,得到的密文组一般与明文等长。其作用于n位明文分组上,产生的自然是n位密文分组;因此分组过小时很容易被统计分析方法攻破。当分组规模相当大的时候明文的统计消息会被掩盖,密码也可以任意选择变换构造,因此这些密码成为“理想分组密码”。但是理想分组密码的密钥规模过大,显然不能在实际中广泛应用。
密码系统的性能可以通过混淆和扩散两个方面来衡量。前者的关键在于使密文的统计特性与密钥之间的关系尽量复杂,后者的关键在于使明文的统计特征消散在密文中(即将明密文之间的统计关系最大程度地复杂化)。因此,引入了Feistel加解密。
Feistel解密过程的结构与加密一致。若将第次加密后的明文分为和这左右两半,则对其再次利用流加密函数进行多轮逐位加密时可以按下方顺序持续循环:
相对应地,若解密过程已经进入第轮,那么此时可以按下方运算继续进行解密:
而显然这种加解密过程都是需要知道加密次数的。假设加密过程一共有轮,那么必然有
换言之,某次加密后的明文左右两部分交换之后左半部分会等于此次变换之前的右半部分,也会等于从反方向解密而来的密文的左半部分或其此次解密之前的右半部分。除此之外还有
在代入为加密过程中的值后可以得到
因此,Feistel结构中的第轮解密后的左右两半一定与加密过程中第轮后的一致。
DES通过56位密钥来加密64位的数据。其会经过初始置换和初始逆置换两次置换,随后在生成的轮密钥控制下进行16轮基于Feistel的迭代加密。DES加密算法除了S盒之外的算法均为线性,而S盒提供了密码算法所必须的混乱作用。S盒的分析难度为这套加密算法提供了非常高的安全性。
明文或者密钥中哪怕只变化一位都会导致密文中很多位都发生变化;这种效应也称为「雪崩效应」。
代数基础
基于离散数学关于逆元、群、交换群、环、可交换环、整环和域的知识继续讨论。
Euclid算法
一种通过递归来实现的最大公约数算法。下面给出通过C语言实现的一种Euclid算法函数模板,就能明白其原理。
1 | int Euclid(int a, int b){ |
如果与的最大公约数是1,那么一定存在使。这个也称为模的乘法逆元。
现在给出一个利用Euclid算法计算最大公约数的例子。
计算1970与1066的最大公约数。
用Euclid算法的求法如下:
因此这两个数的最大公约数是2。
现在考虑如何利用Euclid算法求取余运算的逆元。
求81 mod 28的逆元。
首先对81和28用Euclid方法作如下处理:
因此这两个数互质。另一方面,
因此所以就是81 mod 28的逆元;用这个等式还可以得到,对应的是28 mod 81的逆元。
多项式运算
如果系数在上且次数小于等于的所有多项式共同组成一个集合,那么这个拥有个不同多项式的集合就称为代数系统载体。
现在考虑。对于一个确定的有限域,多项式的乘法在完成了简单的乘法后需要对次数不少于的各项对取模。下面以为例进行简单的解释。
GF(23).
首先结合定义可以知道这个集合里应该是所有系数在中且次数不大于的多项式。显然可以发现不能由这个集合里的任何两个多项式相乘得到,因此这个式子就可以作为不可约多项式。
现在以和为例讨论这个集合上的多项式加、乘法。显然
但此时一次项的系数不在内,因此实际上
现在再考虑乘法。
而不在中,所以常数项循环至;因此知道乘法的结果是。
现在考虑的逆元。显然刚刚已经知道
故而只要求与的最大公约数即可。
因此与互质。而由上方分析又可知道
其中划线的对应需要根据之前求公约数时的等式展开的项。因此
而不是中的项,所以循环移动到,对应项也要改为。因此逆元是。
AES加密
采用宽轨迹策略来抵抗差分分析和线性分析。
轮函数分别经过字节代替(利用S盒中的映射将输入转换为输出)、行移位(对输入状态矩阵的每一行循环左移一定字节)、列混淆(对输入状态矩阵的每一列左乘一个列矩阵)和轮密钥加(将输入和轮密钥异或得到输出)这四个步骤。其中S盒可逆,所属字节代替步骤是AES加密中唯一的非线性运算;最后一轮的加密没有列混淆操作。
分组密码工作原理
中间相遇攻击
考虑一个双重DES加密。顾名思义有加密公式和解密公式,密钥长度位112位;那么这两次DES加密的中间产物显然与和都相等。这时运用所有可能的密钥分别尝试加密明文和解密密文,并分别与比较;若相等则获得了一组可能的密钥对。这时尝试其他新的明密文组合进行进一步验证;根据概率论,在此条件下与第二组明密文对进行比较后筛选剩下的密钥正确的概率是1-2-16;再比较一组进行筛选后所得的密钥正确的概率上升到了1-2-80。以此类推,找到正确密钥的时间复杂度仅为,而单次DES加密找到正确的密钥对应的时间复杂度也不过。
事实上,中间相遇攻击并不依赖于DES的性质。DES只是一个典型的分组密码;中间相遇攻击对所有的分组密码都适用。
多重DES加密
现在考虑三重两密、三重三密、五重三密这三种常见多重DES加密的思路。
三重两密
处理明文时涉及两个加密密钥,采用的思路进行加密。
这个思路可以适应单DES——当且仅当时这个三重加密算法和一重加密一致。目前,这个思路还没有可行的攻击方法。
三重三密
处理明文时涉及三个加密密钥,每次处理所用的密钥都不同。思路本质上是.
这个思路的应用比较多——PGP和S/MINE都使用这种多重DES加密思路。
五重三密
处理明文时涉及三个加密密钥,遵循等式。
这种思路可以适应三重两密的情形,因此也可以适应单DES。
分组密码工作模式
DES加密在明文的最后一个片段不足分组长度时会补上0/1/随机串。
电码本(ECB)
经常应用于单个数据的安全传输。
结合加解密公式可以知道这种模式下密文中某位出错后只会影响这一位明文的恢复,所以这种加密算法不会传播错误。
密文分组链接(CBC)
在对长度大于64位的明文进行加密时会考虑使用。
由于加解密会涉及到相邻的位,所以如果密文传输过程中有一位出错会导致明文中它的后一位也会出错,进而造成多米诺效应。因此,这种加密算法会传播错误。
密文反馈(CFB)
加密长度大于64位的明文时会考虑使用。这种工作模式比较保密且分组随意,可以作为流密码使用。
这种模式的错误传播比CBC更厉害。当密文的第位在传输过程中出错后,其后的位都会收到影响。其中,是明密文的位数。
输出反馈(OFB)
噪声信道上传输数据流(如卫星通信等)常用的工作模式。这种工作模式抗攻击能力不如CFB,但是错误不传播。
计数器模式(CTR)
用于分组高速传输。这种工作模式可以并行处理加密,硬件效率非常高,加之整个加解密过程只涉及加密函数而不涉及解密函数,这个工作模式是非常理想的。
其中是计数器初值。这个模式的错误不传播。
随机数和流密码
密码学意义上的“随机”指的是不能预测。一般还有“真随机”(不能重复产生)和“伪随机”(看上去随机且能通过一部分随机性测试)两种随机;密码学中应用的随机数至少需要是强伪随机数,即满足随机性和不可预测性。
当一个伪随机数生成器的均匀性(0和1出现率大致相等)、可伸缩性(任何子序列都能通过随机性测试)和一致性(对所有种子产生的序列和这些序列的子序列都应该通过随机性测试)较好时,这个发生器较好。
已知一个周期为的序列,当存在使任意都有时这个序列也是终归周期序列。
伪随机数发生器
将一个短的随机数“种子”扩展为较长伪随机序列的确定算法称为伪随机数发生器。根据原理分为“基于数论方法的”和“用加密方式的”两种;前者包括线性同余发生器和BBS发生器,后者包括对称和非对称加密算法及Hash函数与消息认证码。
RC4流密码
一种面向字节操作的流密码,密钥长度可变;广泛应用于Web SSL、TLS、Wi-Fi WPA、IEEE 802.11 WEP等现实场景。其中消息的处理以字节为单位,以流为进行方式,使用伪随机密钥流与明文进行按位异或运算。重复使用这个密钥流会导致被破译。
数论基础
费马小定理
若是不能整除的素数,那么
这句话也可以理解成“对正整数和质数一定有”。这个结论可以大幅度简化求余运算,但有自身的局限性——当且仅当为质数时才能用此定理。
欧拉定理
记为小于且与互质的正整数个数,那么称为欧拉函数。
欧拉函数有如下性质:
- ;
- 为素数时;
- ;
- 且与均为质数时;
- 若,那么。
欧拉定理:若与互质,则
欧拉定理凭借模数可以为非质数的优势比费马小定理更加通用。
求2100 mod 35。
显然因为模数35不为质数所以无法使用费马小定理。现在记,那么。因此
离散对数
根据欧拉定理一望而知,任意都存在对应的,使。这样的的最小值称为的阶(或关于模运算的指数或周期)。
若的阶为,则称是的本原根。对于一个质数的本原根,显然的值各不相同。
若任意整数和模数的本原根有唯一的指数使,则称为以为底、模为的的离散对数,记作。
公钥密码学·RSA
一个拥有n个用户的系统两两之间都需要利用对称加密进行保密通信,则显然需要C2n个密钥,每个用户有n-1个密钥。
显然对称密码的弱点在于密钥量大且管理困难。网络中的签名、认证等应用也无法通过对称加密实现;因此考虑非对称密码。
公钥密码通信的过程主要依靠加密和解密两个不同的密钥来完成。收信人Alice在设计两个密钥之后将加密密钥公开给发信人Bob,后者利用这个加密密钥将自己的信息转为密文,随后发送给Alice;Alice收到密文后利用自己所保存的解密密钥进行解密,得到信息明文。
在这个过程中,最关键的部分其实是密钥的设计;RSA非对称加密根据欧拉函数,利用2个大素数就可以完成。Alice先选择两个大素数和,之后得到和;随后选择一个与互质的数作为加密密钥,计算作为解密密钥。随后Alice会将和公开给Bob,自己留存;Bob遵从等式进行加密的同时Alice遵从即可实现成功的加解密。
公钥密码学·其他体制
Diffie-Hellman密钥交换
现有大素数和模数的本原根公开在世界。那么手握随机数的Alice可以经过计算得到公钥并将其发送给手握随机数的Bob;Bob也可以通过一样的手段将发送给Alice。此时两人分别计算密钥值和;显然两人得到的密钥相等且均为。这时,两人完成了一次成功的密钥交换。
现在假设一个人在Alice和Bob中间。它在截获了和之后可以经过任意的篡改让Alice和Bob同时收到相同的信息;对应会导致两人得到的密钥分别是和,可能不相等。这次中间人攻击之所以能够实现正是因为Diffie-Hellman密钥交换中没有提供密钥认证功能。
ElGamal密码
现有大素数和模数的本原根公开在世界。这时选择随机数并计算并公开,那么加密期间可以通过随机选择一个与互质的整数计算和得到密文;解密过程则可以利用自己保管的根据密文计算得到明文。
Hash函数
对任意长度明文进行变换所用的一个函数。变换后的函数值也称为散列值,其长度一般固定。
Hash函数一般用于消息认证码、数字签名的预处理和口令衍生密钥等领域,其无法求逆且对给定很难找到使成立的,也很难找到任意一对与使。换言之,Hash函数同时具备抗原像攻击性(单向性)、抗弱碰撞性和抗强碰撞性。
(生日悖论)一个房间内有k人,当k多大时其中存在两人有相同生日的概率大于0.5?
个人的生日排列总数一共有个,有不同生日的排列总数为。因此需要使,解得。
用上述方法也可以得到当时有两人同生日的概率为0.99999997,已经很接近必然事件了。类似地,Yuval提出了对Hash函数的生日攻击方案。攻击者产生一份合法明文后产生个不同的变形,并将其作为一个合法的明文组。随后其生成一份非法明文按上述方式产生一个非法明文组;分别对以上两个组产生散列值,在两组明文中找出散列值相同的一对。这时攻击者就找到了与合法明文具有相同散列值的非法明文;如果没有找到可以在增加每组明文的变形个数,直到找到。显然根据刚刚“生日悖论”的结论这很难不成功。
消息认证码
单纯的加解密算法是无法保证能够抵抗伪装、内容修改、顺序修改、计时修改和收发方否认这五种攻击的。这些攻击本质上属于数据完整性范畴而不是机密性范畴;对于前四个可以用消息认证码(MAC)来解决。
MAC本质上是密码校验和,信息的长度可变,但是密钥需要保密且收发双方共享。这种认证码长度固定;很多消息会对应同一个MAC值,但找到这个MAC值所对应的多个消息很困难。
一般通过函数对消息运用密钥进行加密。有时加密算法会改为Hash函数,因为Hash函数较快且没有出口限制。这种基于密码的Hash函数的消息认证码称为HMAC;由于hash函数并不依赖密钥,所以不能直接用在MAC上。
数字签名
一般基于RSA。在利用私钥计算完后发送给收信方,收信人会利用公钥计算与是否相等。如果不等于就意味着信息有误,因此会被拒绝。需要注意的是如果攻击者有能力进行模的大整数分解,那么它很容易就能计算并且进而利用Euclid算法得到发信者签名时所用的私钥。因此,发信人要谨慎选取与。
认证协议
重放攻击
把有效的签名信息拷贝后重新发送给收信方。
针对这种攻击方式可以通过时间戳、序列号和随机数的方式来解决。其中后者目前最为常用,时间戳则需要同步时钟。
Needham-Schroeder协议
有第三方(KDC)作为中介参与的密钥分发协议。协议包括A到第三方、第三方到A、A到B、B到A和A到B一共五个步骤。
Denning AS协议
有第三方(AS)作为中介参与的密钥分发协议。协议包括A到第三方、第三方到A、A到B三个步骤;会话密钥由A选择所以不会被AS泄密。这个协议需要依靠时间戳来防止重放攻击,因此需要时钟同步或者临时交互号。
Kerberos
分为认证服务器(AS)和票据授权服务器(TGS)两个服务器。前者在初始时与用户对话,使用户验证身份,随后发放高度可信的「票据授权票据」(TGT);用户持TGT才能在后者得到访问其他应用服务的票据。
票据除了TGT之外还有「服务授权票据」(SGT)。TGT是客户访问TGS服务器时所需要提供的票据,目的是为了申请某一个应用服务器的SGT;SGT在客户请求服务时由服务器提供。访问TGS服务器的票据(Tickettgs)在用户登录时向AS申请一次即可,可以多次重复使用。
在Kerberos的身份验证过程总共3步。客户端与身份认证服务器先进行互相的身份验证,随后客户与票据授权服务器进行互相的身份验证。之后客户端与服务器进行互相的身份验证,为客户端提供服务。
传输层安全
SSL协议
一种在两个端实体之间提供安全通道的协议。其提供了通道级别的安全——这两端知道所传输的数据保密且没有被篡改。
SSL主要包括记录和握手两个主要协议。前者建立在可靠的传输协议(如TCP等)之上来保证保密性和完整性,并用来封装高层协议;后者用于客户和服务器之间的相互认证与有关加密算法和密钥的协商,提供了连接的安全性。SSL记录协议传输的是安全记录,将数据流分割成了若干个片段并单独进行保护与输送;SSL握手协议则会在完成安全相关协商后交换证书和相应密码信息以便身份认证。产生主密钥后其会将安全参数提供给SSL记录层,检验双方是否已经获得了同样的安全参数。
SSL握手
主要包括建立安全协商、服务器认证和密钥交换、客户端认证和密钥交换和完成四个步骤。
在第一个阶段,客户会发送包括协议版本、会话ID、客户支持的密码算法列表、客户支持的压缩方法列表、初始随机数(32位时间戳+28字节随机序列)在内的client_hello信息;作为反馈,服务器会发送包括客户端建议的低版本以及服务器支持的最高版本、会话ID、客户支持列表中选出的密码算法和压缩方法、服务器产生的随机数在内的server_hello信息。
在第二个阶段,服务器会发送一个含有X.509证书(或一条证书链)的certificate信息,之后选择性地发送server_key_exchange、certificate_request,最后发送server_hello_done等待客户端应答。certificate除了匿名Diffie-Hellman密钥交换之外的其他交换方法都需要提供;server_key_exchange在证书消息没有包含必需的签名、被签名内容中的随机数或服务器参数时才会发送。
在第三个阶段,客户开始验证服务器证书。其将检查server_hello消息参数是否可接受;若无问题则发送至少一条消息给服务器。如果服务器请求证书,则客户首先发送certificate消息;若客户没有证书,则发送无证书警报。在这之后客户根据密钥交换的类型发送client_key_exchange消息,最后选择性地发送包含一个签名的certificate_verify消息。
在第四个阶段,客户发送change_cipher_spec消息,将协商得到的密码规范复制到当前连接的状态,随后用新协商的算法和密钥参数发送finished消息,可以验证密钥交换和认证过程是否成功。其中包括的校验值会对所有握手消息进行校验。服务器同样会发送这两个名字的消息;至此握手过程完成,客户和服务器自此可以交换应用层数据。
IPSec
IP安全性在协议部分分为认证头(AH)和封装安全性有效载荷(ESP)。密钥管理部分有SA、ISAKMP和IKE三个;ISAKMP定义了密钥管理框架,IKE是目前正式确定用于IPSec的密钥交换协议。
IPSec在IPv6中强制,在IPv4中可选。
AH和ESP都同时支持传输模式和隧道模式;这两个模式中前者为上层协议提供保护,后者保护整个IP包。AH是认证的扩展报头,ESP是实现加密(也可选择认证)的扩展报头。
为了结合认证和机密性,目前主流采用的是传输邻接和传输隧道束两种组合。前者使用两个捆绑的传输SA,内部是没有认证选项的ESP SA,外部是AH SA;后者的组成为内部AH的传输SA+外部ESP的传输SA,在加密之前就进行了认证,更加可取。
ISAKMP定义了建立、维护、删除安全关联(SA)的过程和包格式,也定义了生成交换密钥的载荷和认证数据。其独立于特定密钥交换协议、加密算法、认证机制。作为一个针对认证和密钥交换的框架,其协商分为建立ISAKMP SA和针对其他安全协议的SA两个阶段。
实验报告
实验一 古典密码实验
实验目的:了解并掌握Caesar密码、仿射密码和单表置换密码的加解密原理。
Caesar密码
自选语言设计Caesar算法,并能任意指定英文字母组合和密钥对前者进行加密。
实验原理
Caesar加密/解密是一种替换加密技术,明文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后被替换成密文。例如,当偏移量是3的时候,明密文对照表可以如下所示:
| 明文 | ABCDEFGHIJKLMNOPQRSTUVWXYZ |
| 密文 | DEFGHIJKLMNOPQRSTUVWXYZABC |
实验代码与运行记录
加密算法
显然根据实验原理中所描述的定义和思路不难得到凯撒密码的加密算法。为了区分英文字母的大小写,大写字母的加密结果会变为小写,而小写则会被加密为大写。
算法中暗含了一个隐形的“明密文对照表”。英文Caesar密码的解密过程本质上是将密文进行新一轮加密,只是发生了反向的偏移。换言之,加密的偏移量和解密时的偏移量在处理英文文本时显然有。利用此即可通过语言kotlin得到如下所示的算法代码。
1 | private fun caesarCipher(text:String, key:Int, decryptMode:Boolean): String { |
运行结果
对该算法代码设计主程序的输入、输出。随后运行该程序;以加密时偏移量为5,并对文本“Hello”进行加密的情况为例,运行结果如下所示。
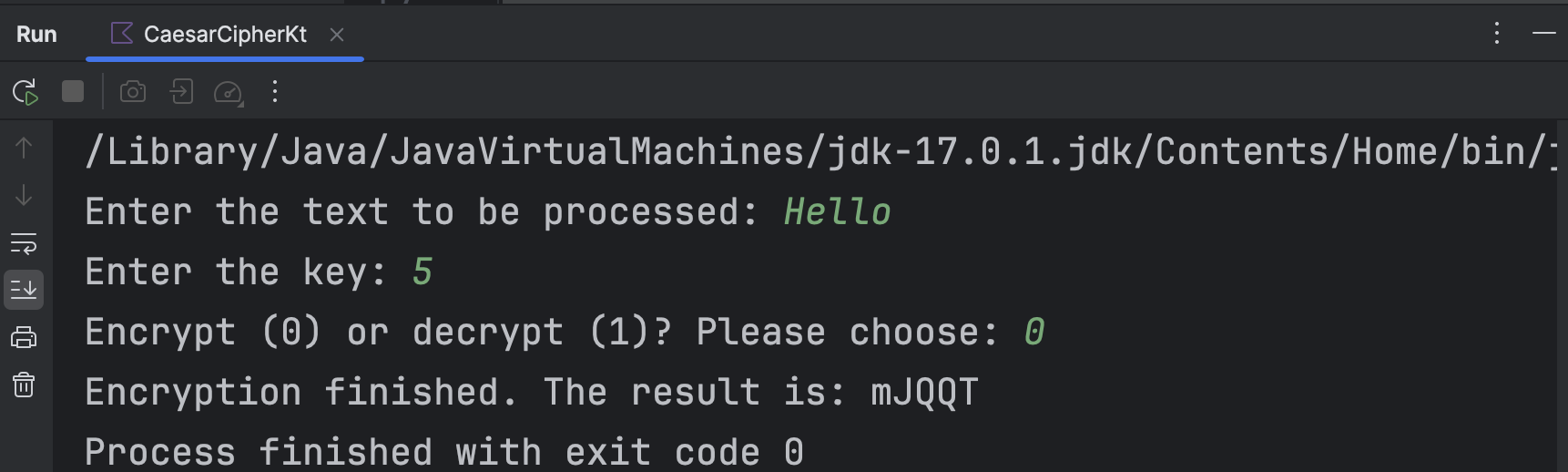
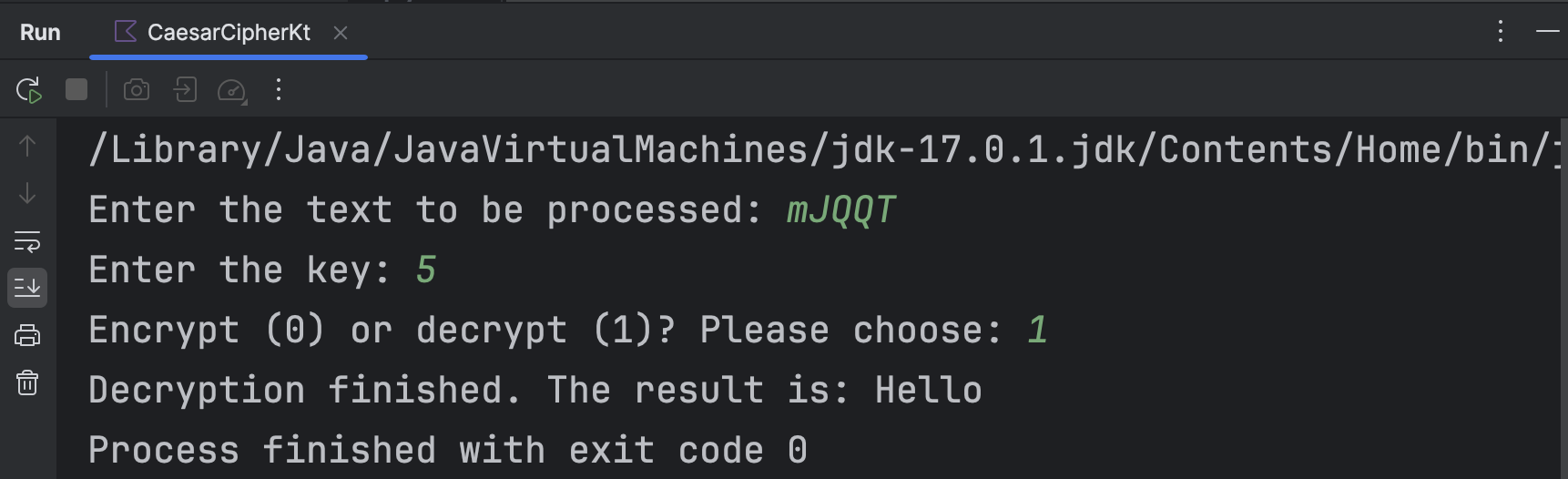
显然解密结果与原本的明文一致。
仿射密码
自选语言设计算法,使该算法能够对任意英文字母组合和密钥进行仿射加密。
实验原理
仿射密码本质上与Caesar密码类似,也是一种替代加密技术。对总字母数量为的语言体系中的任意字母,其加密后的结果满足,其中是与互质的任意值,是任意值。
与加密函数相对应地,解密函数为,其中是的一个取模倒数。
显然可以通过等式
证明加密结果的解密结果就是原文本身。
实验代码与运行记录
算法代码
根据上方定义不难得到仿射加解密的算法。在讨论算法之前,首先要对算法中等式的一部分参数进行设计。
首先要确保与互质。
1 | private fun isPrior(a:Int,b:Int):Boolean{ |
然后生成的取模倒数;此值应能确保与的乘积对的求余结果为1。
1 | private fun inverseGenerator(a:Int,m:Int):Int{ |
这时考虑加密。由于是英文字母分大小写总共52个,故不妨令。在这之后先生成一个暗含的明密文对照表cipherSheet,再根据此表通过ReferenceForIndex对每一个给定的字符查找到该字符在表中所对应的索引;类似地,再通过cipherSheetReferenceForChar可以找到特定索引号在表内所对应的字符。之后根据上述所有函数利用定义即可用kotlin写出算法代码如下所示。
1 | private val cipherSheet=CharArray(55) |
运行结果
根据算法代码设计输入输出,并运行该程序。以利用对明文“Hello”进行加解密为例,得到的结果如下所示:
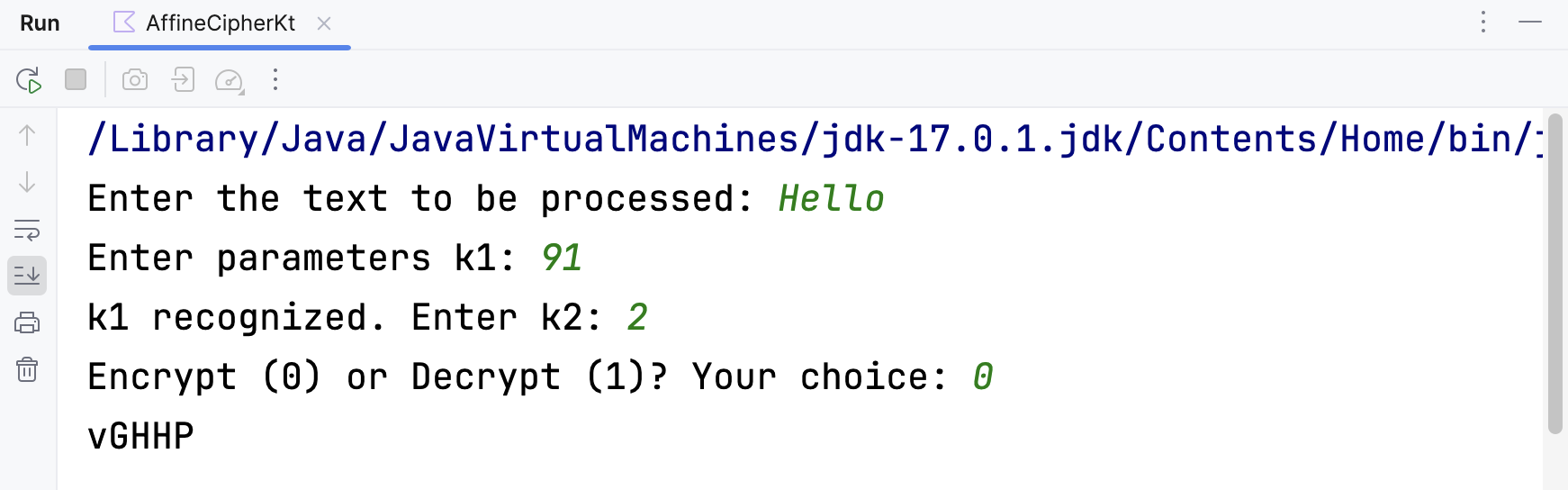
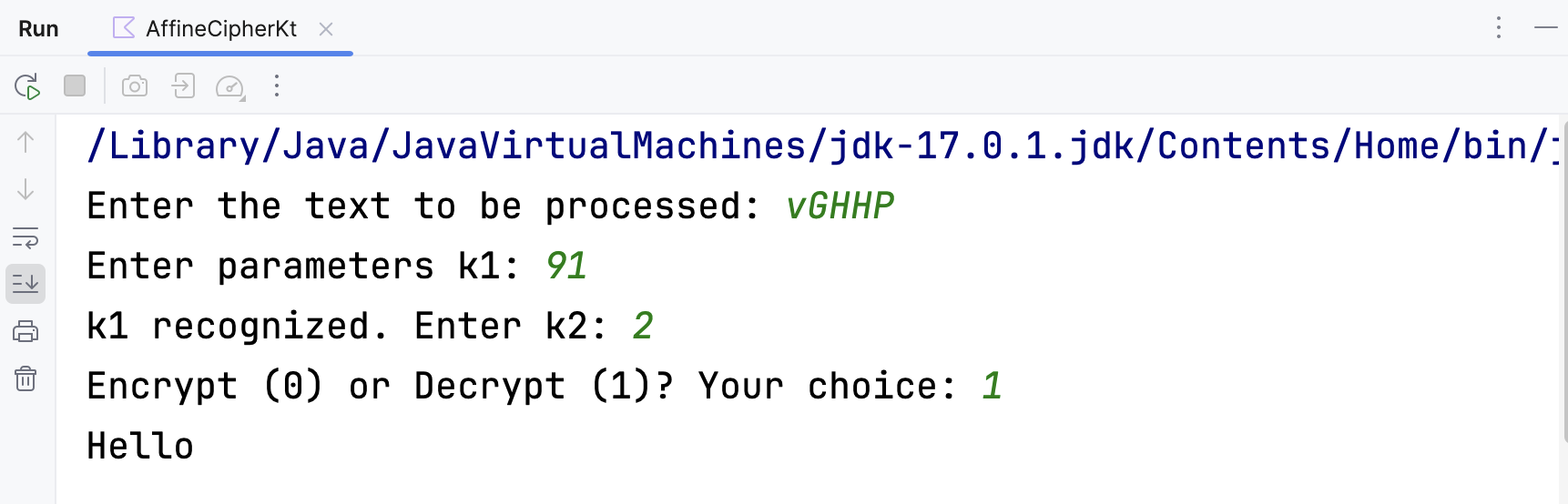
可以看到,解密的结果与原本的明文一致。
单表置换加密
自选语言设计算法,使该算法可以对文本进行单表置换加解密。
实验原理
单表置换加密本质上是一种置换式加密;与替代式加密的不同之处在于,其可以通过打乱明文(通常是字符或字符组)中的各字符所处的相对位置而实现加密,并在打乱后生成文本密文。在没有密钥的情况下,生成的消息极难破译,因为字符有意义的排列方式可以有很多种。
单表置换加密算法中维护着一个置换表,其中记录了明文和密文的对照关系。在没有加密(即没有发生置换)之前,其置换表可以如下。
| 明文 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 密文 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 明文 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 密文 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 明文 | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 密文 | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 明文 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 密文 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
在设定密钥为“Munich”后,置换表将发生改变;改变后的结果如下。
| 明文 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 密文 | m | u | n | i | c | h | a | b | d | e | f | g | j |
| 明文 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 密文 | k | l | o | p | q | r | s | t | v | w | x | y | z |
| 明文 | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 密文 | M | U | N | I | C | H | A | B | D | E | F | G | J |
| 明文 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 密文 | K | L | O | P | Q | R | S | T | V | W | X | Y | Z |
比较后不难看出两置换表之间的区别。选用的密钥“Munich”将小写字母置换表区域中的m、u、n、i、c、h按密钥中的顺序提前至首位,剩余的未出现在密钥中的字母按字母表顺序排列在小写字母置换表中的剩余位置。大写字母置换表区域与其一致。
实验代码与运行记录
算法代码
和仿射加密类似,算法中暗含了一个加密对照表和一个解密对照表。在加解密的过程中,只要通过对字符查找索引和根据索引查找字符即可实现置换。据此可以通过kotlin写出算法如下。
1 | private val encryptSheet= IntArray(30) |
运行结果
根据上述算法设计输入输出。以采取密钥“Munich”对明文“Berlin”进行加解密为例,可以得到运行结果如下所示。
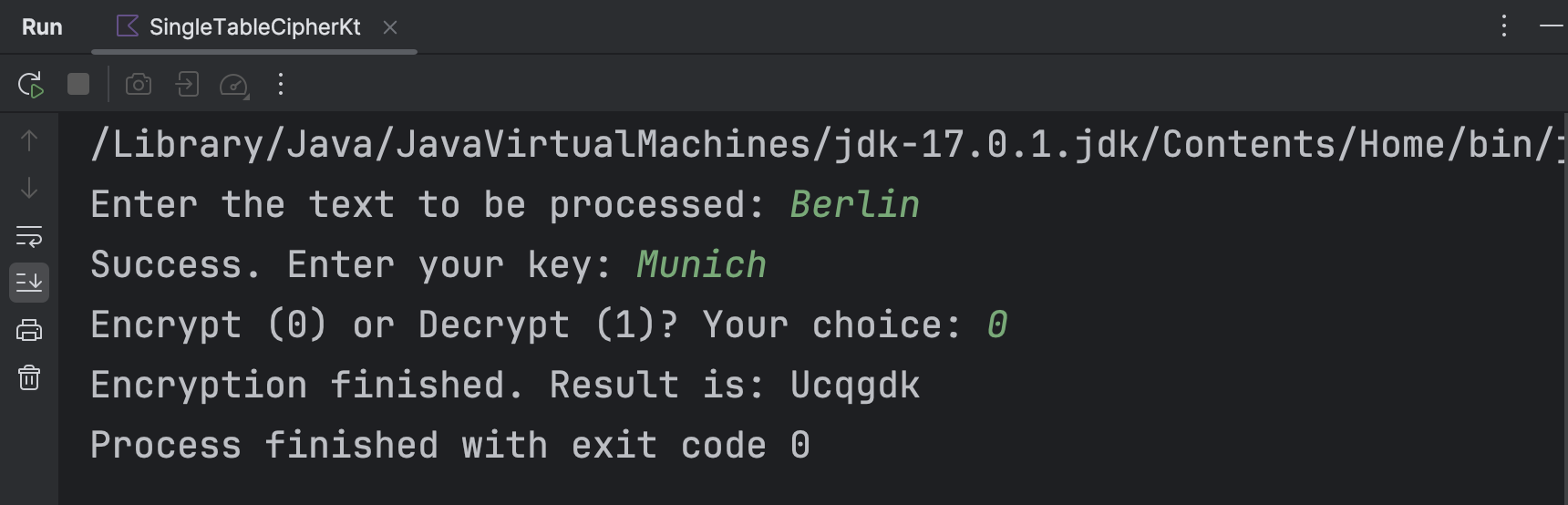
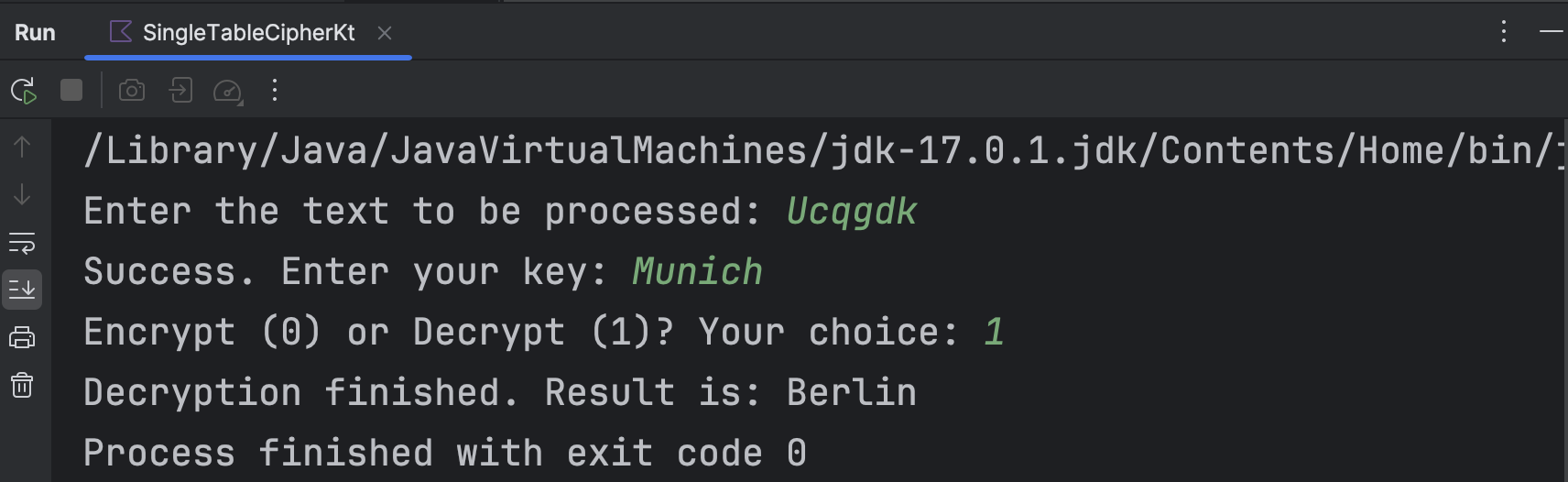
显然,解密结果和原本的明文一致。
实验心得
古典密码学的各种加密都是通过简单的表内对照或基本运算实现的。也正是因此,这些加密算法都非常容易被破解;只有密钥相对复杂的置换式加密才有可能存在破译难度。
算法的编写过程中完全根据定义就能写出,没有遇到什么困难——这也比较符合这些密码广为使用时的实际场景。
实验二 对称密钥加密(DES)实验
实验目的:了解并掌握DES加密的基本思路和加密算法。
实验内容:自行选取语言编写算法,使该算法在不使用该语言自带的加密库的情况下能够对给定文本进行加解密。
实验原理
数据加密标准(英语:Data Encryption Standard,缩写为DES)是一种基于使用56位密钥的对称密钥加密算法,1976年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),随后在国际上受到广泛使用。算法的整体结构中有16次相同的循环处理过程;在主处理这些循环之前,待加密的文本会被分成两个32位的半块后分别处理;这种交叉的方式也被称为Fiestel结构。Fiestel结构保证了加解密过程的相似度,唯一的区别在于子密钥在解密时是应用顺序与加密时相反。
在对这两个32位的半块做处理时主要包含以下四个步骤:
- 扩张:用扩张置换将32位的半块扩展到48位,其输出包括8个6位的块,每块包含4位对应的输入位,加上两个邻接的块中紧邻的位。
- 密钥混合:用异或操作将扩张的结果和16个48位的子密钥中的每一个进行混合;这些子密钥都是利用密钥调度从主密钥生成的。
- S盒:在与子密钥混合之后,块被分成8个6位的块,然后使用“S盒”(或称“置换盒”)进行处理。8个S盒的每一个都使用以查找表方式提供的非线性的变换将它的6个输入位变成4个输出位。
- 置换:将S盒的32个输出位利用固定的“P置换”进行重组,从而将每个S盒的4位输出在下一次循环中的扩张步骤时使用4个不同的S盒进行处理。
在上方密钥混合步骤中所提到的“密钥调度”主要先使用选择置换1(PC-1)从64位输入密钥中选出56位的密钥。剩下的8位要么直接丢弃,要么作为奇偶校验位。然后,56位分成两个28位的半密钥;每个半密钥接下来都被分别处理。在接下来的每次循环中,两个半密钥都被左移1或2位(由循环次数数决定),然后通过选择置换2(PC-2)产生48位的子密钥——每个半密钥24位。移位表明每个子密钥中使用了不同的位;每个位大致在16个子密钥出现14次。
处理之后将结果与另一个半块异或。在此之后将得到的结果与原本的半块组合并交换顺序,进入下一次循环。在最后一次循环完成时,两个半块需要交换顺序。
实验代码与运行结果
算法代码
根据上述定义利用python语言作代码如下。
1 | import time |
运行结果
根据上方算法设计输入输出,并运行该程序。以利用八位密钥“DESCrypt”加密文本“Hello DES”为例,得到加解密情况如下:
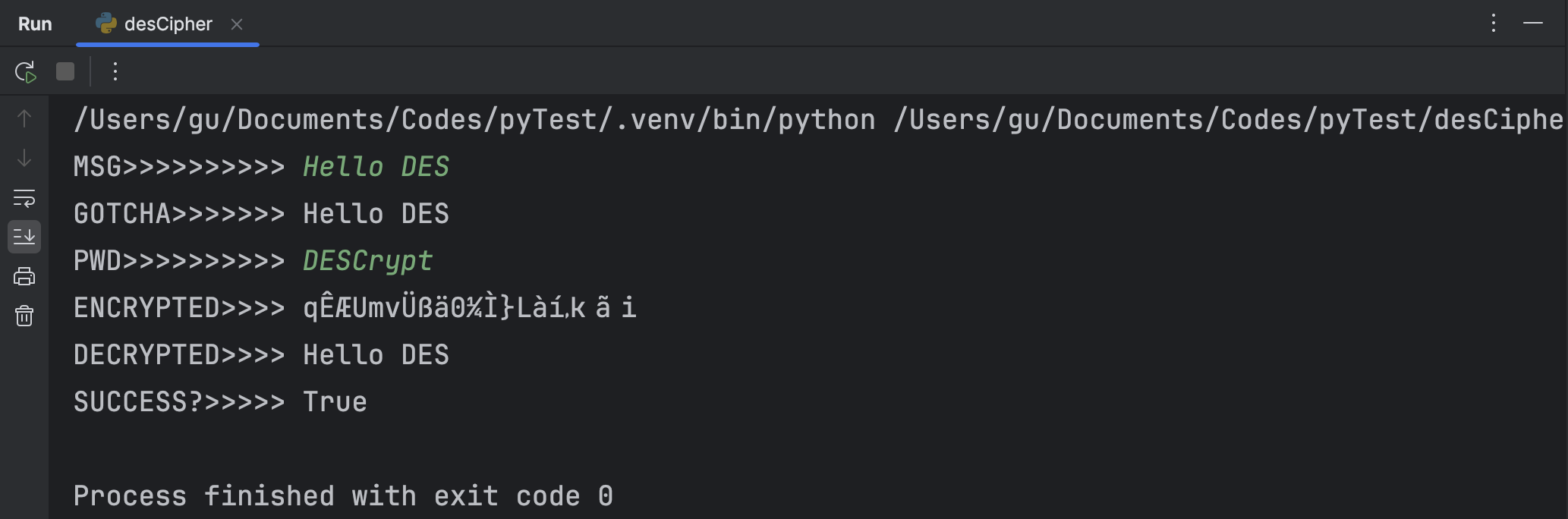
显然解密得到的文本与加密前一致。
实验心得
作为一个已经有了完整体系且至今仍受欢迎的加密算法,DES加密算法的代码量非常大。为了降低转码的工作量,选取了中英文字母都占2个字节的Unicode作为文本处理后的第一步。
实验三 非对称加密(RSA)实验
实验目的:了解并掌握RSA加密算法的原理。
实验内容:自行选取语言编写算法,使该算法在不利用该语言自带密码库的情况下能够对文本进行RSA加解密。
实验原理
RSA加密算法是一种非对称加密算法,在公开密钥加密和电子商业中被广泛使用。
公私钥
若Alice想要接收Bob的私人訊息,她可以用以下的方式來产生公钥和私钥:
- 选取任意两个较大且不相等的质数和,并计算。
- 根据欧拉函数求
- 任取一个小于且与之互质的整数,并求关于的取模倒数。
通过此方法得到的数对即公钥,即私钥。Alice自己保留私钥的同时将公钥发送给Bob即可开始使用非对称算法的加密信息传送。
信息加(解)密
假设Bob想在知晓Alice生成的和的情况下给Alice发送消息,则Bob只需要将中的每一个字通过unicode或其他转码方式转换为一个小于的非负整数,随后通过公式将信息加密为密文,再将发送即可。Alice收到消息后解密的方式也类似,只需要利用和她的私钥通过公式得到原文即可。
显然可以证明
若与互质,则由欧拉定理显然有
否则不妨设,进而有
故
实验代码与运行结果
利用语言kotlin编写算法如下。
1 | import kotlin.random.Random |
根据上述代码设计输入输出如下。
1 | private fun main() { |
运行该程序。以利用质数41、281加密明文“Hello RSA”为例,运行结果如下图所示:
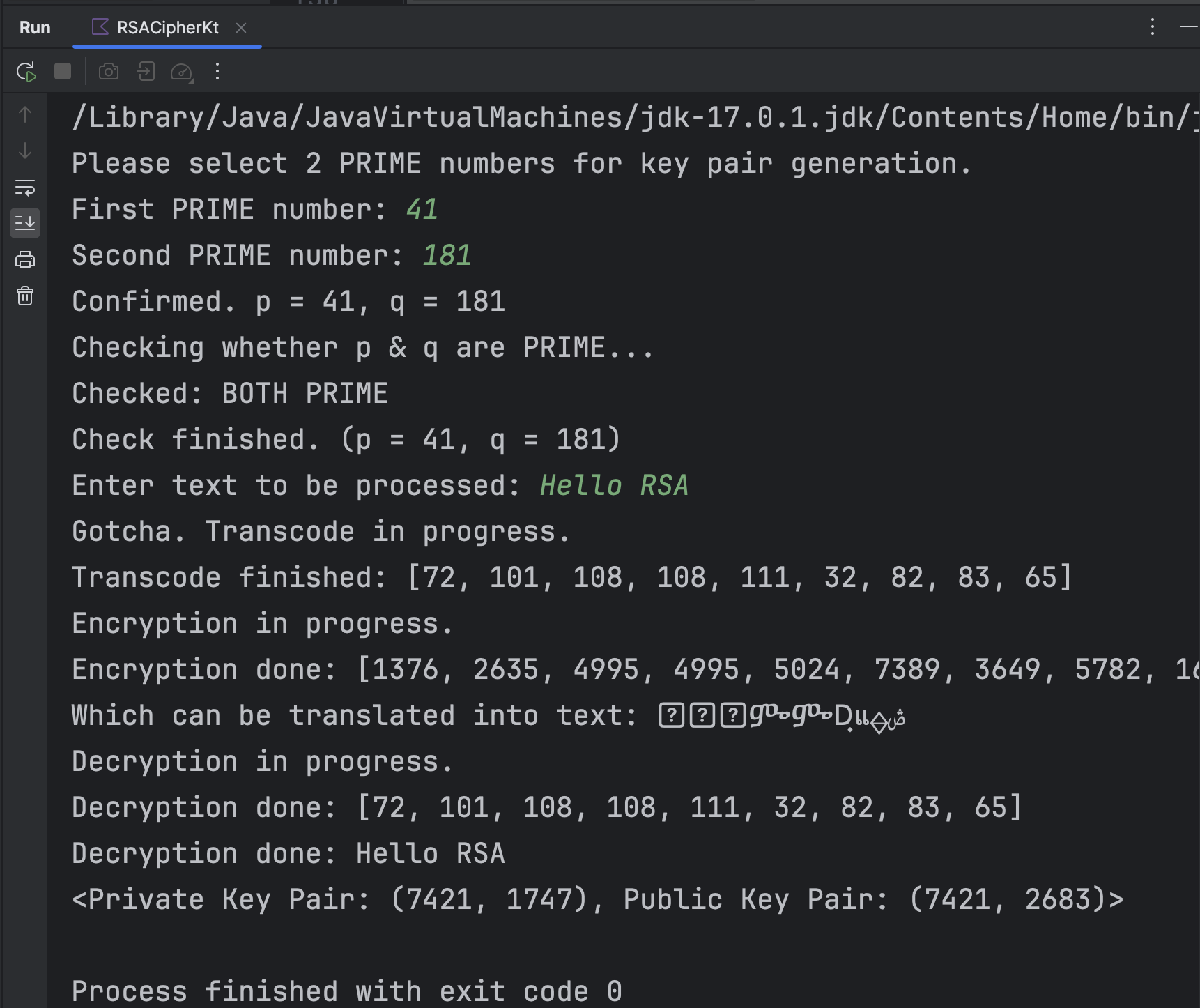
显然解密结果与原文一致。
实验心得
根据RSA实验原理定义,对极大整数做因数分解的难度决定了RSA算法的可靠性——对一极大整数做因数分解愈困难,RSA算法愈可靠;如若后期有人能够找到一种快速分解质因数的算法,那么用RSA加密的信息的可靠性就会骤降。
实验四 MD5加密实验
实验目的:了解并掌握哈希加密算法的工作方式。
实验内容:自行选择语言编写算法,使该算法在不利用该语言自带密码库的情况下可以实现对文本的MD5加密。
实验原理
MD5消息摘要算法是一种被广泛使用的密码散列函数,可以通过求余、调整长度等方式产生一个特定长度的的散列值来确定信息传输始末内容的完整性和一致性。经过程序流程,MD5加密算法可以生成四个32位数据,最后联合起来成为一个128-bits散列。
实验代码与加密结果
通过python编写的加密程式如下所示。
1 | import math |
运行该程序。以加密文本“hello md5”为例,得到散列值如下所示:
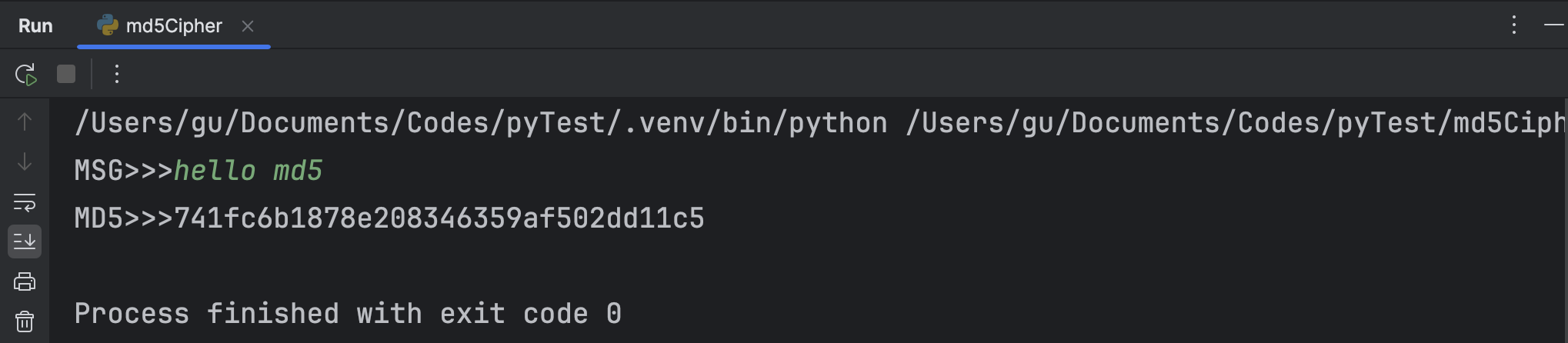
在其他网站上使用在线md5加密工具,加密同一个文本,得到的散列值与之相同。
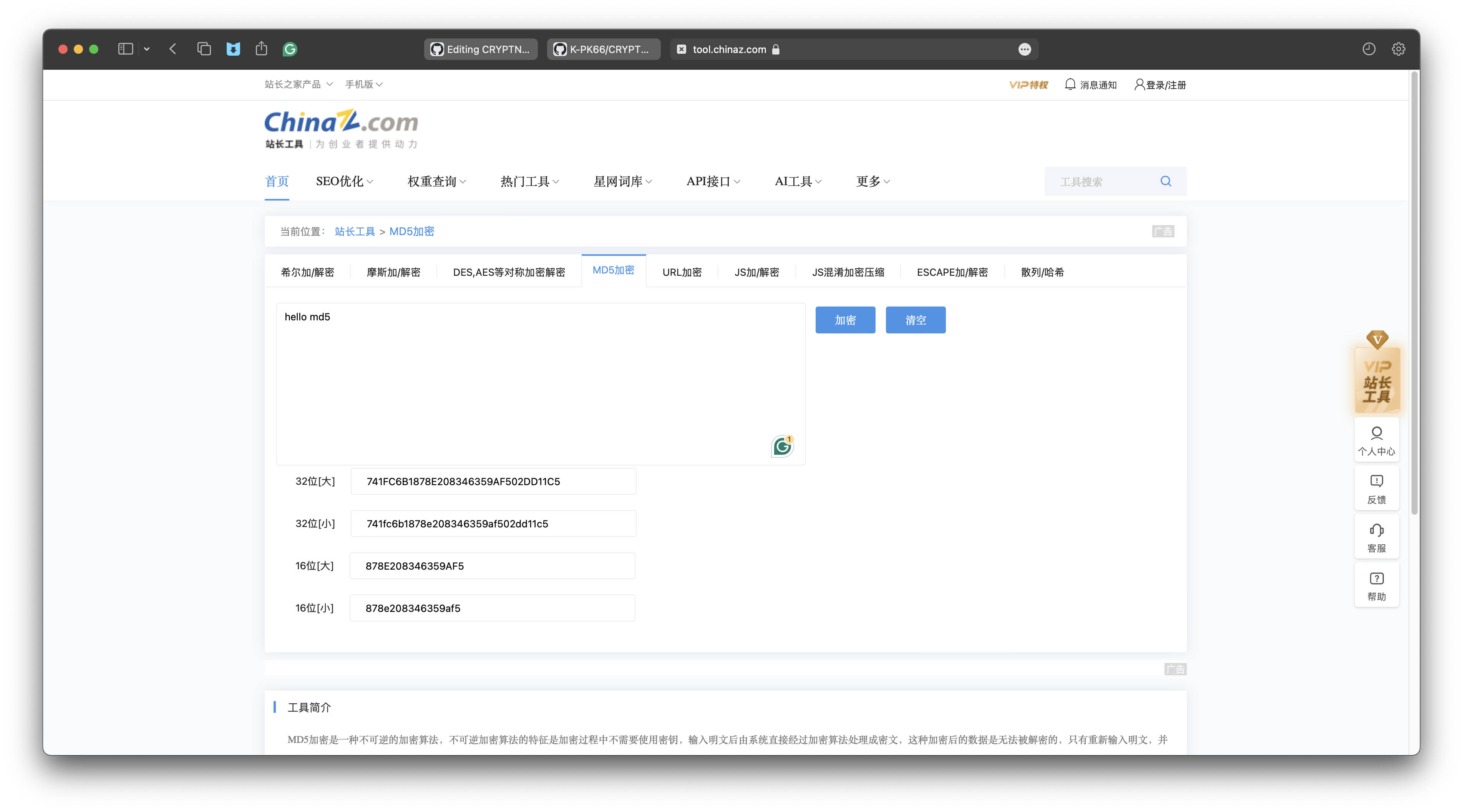
因此,编写的算法是正确的。
实验心得
MD5作为验证被传输信息完整性和一致性的散列值生成方式,其算法也很难被模仿出来,因此代码量也非常的大。在16进制与10进制数相互转换的时候很容易因为疏忽而错转漏转。
实验五 密码学应用·文件加密传输试验
实验目的:掌握对称加密、非对称加密和哈希算法生成散列值的使用场景并能灵活应用这三种加密方法。
实验内容
自选语言编写代码文件若干,使这些程式在不借助这些语言自带密码库的情况下能够模拟文件的加密传输与解密且保证满足信息传输的诸多基本要求(如不可否认性、完整性等)。标注清楚发送端需要发送的文件和这些文件的产生方式,并说明接收端接收到的文件和之后的处理方式。发送的文件须打包发送。
功能实现
根据实验内容主要考虑以下几个方面。加密算法的代码在前文均已提及,为减少篇幅在此不与呈现。
机制
文件传输最经典的应用莫过于电子邮箱。因此类比电子邮箱的操作,可以将收发信两端简单模拟成一个个人电子邮箱中的sent(已发送)和inbox(收件箱)两个文件夹。注意到实验内容要求对文件进行打包发送,因此考虑电子邮箱中的outbox(待发送)文件夹——其将暂时存储加密之后的文件,在所有文件生成完毕后询问用户是否确定发送(类似于邮件的“确认发送倒计时”操作)。完成发送后,outbox中的文件将全部转移至sent中;如若用户在这一环节取消发送,outbox中的所有文件将会被销毁。
1 | ### fileTransmit.py ## |
此外,注意到收发信两端还可能需要用到的非对称加密,另需要一位作为管理者(keyProvider)的角色为他们分发各自的公私钥。考虑到私钥需要二人自行保管,keyProvider会将私钥private_key_sender.txt和private_key_receiver.txt置于双方各自的沙盒sandbox_sender和sandbox_receiver中作为隔离,公钥public_key_sender.txt和public_key_receiver.txt则将放置在公共空间中。
1 | def individualized_key_pair_generator(client): |
因此整个实验过程应须要inbox、outbox、sent、sandbox_receiver、sandbox_sender五个文件夹。在实验每次模拟开始前,可以对这些文件夹进行适当的初始化,便于在实验进行过程中查看每一步的变化:
1 | ## Python file to initialize the overall progress of the file transmit |
发送方
发送方显然是消息的撰写者和整个流程的开端。他需要对自己撰写的信息进行加密,并且对此次加密所使用的密码也进行加密。随后,他还需要对这两个加密之后的内容都生成散列值,然后对这一散列值进行加密进行发送。为保安全,这三个文件使用同一个加密方式进行加密显然是不行的;加之需要考虑信息传输的基本安全要求,故可分别利用对称加密密钥、发送方非对称加密私钥和接收方对称加密公钥按如下方式进行加密:
1 | message_encrypt() |
- 使用对称加密密钥对信息进行加密,确保文件的机密性(对称加密密钥和信息明文
sample.txt可以直接存储在sandbox_sender中);1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20def message_encrypt():
encrypted_lines = ""
with open('sandbox_sender/desPassword.txt', 'r') as des_password_gotcha:
des_pwd = des_password_gotcha.readline()
with open('sandbox_sender/sample.txt', 'r') as original_file:
original = original_file.read()
original_length = len(original)
if original_length % 4 != 0:
original = original + int(4 - (original_length % 4)) * " "
original_length = len(original)
encrypted_line = ""
for i in range(int(original_length / 4)):
temp_text = [original[j] for j in range(i * 4, i * 4 + 4)]
encrypted_line = "".join([encrypted_line, DES(temp_text, des_pwd, 0)])
encrypted_lines += str(encrypted_line)
## print(encrypted_lines)
with open('outbox/encrypted_msg.txt', 'w') as container_of_encrypted_contents:
container_of_encrypted_contents.write(encrypted_lines)
print("Message has been encrypted.") - 对加密信息所用的对称加密密钥利用接收方的非对称加密公钥进行加密,使接收方无法否认文件由他接收;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16def des_key_encrypt_with_rsa():
with open('sandbox_sender/desPassword.txt', 'r') as des_password_gotcha:
des_pwd = des_password_gotcha.readline()
with open('public_key_receiver.txt', 'r') as pub_key_radio:
public_key_pair_string = pub_key_radio.readline()
public_key_pair_string2pair_step_1 = public_key_pair_string.split(', ')
public_key_pair_string2pair_step_2_a = public_key_pair_string2pair_step_1[0].removeprefix('(')
public_key_pair_string2pair_step_2_b = public_key_pair_string2pair_step_1[1].removesuffix(')')
public_rsa_key_pair = int(public_key_pair_string2pair_step_2_a), int(public_key_pair_string2pair_step_2_b)
rsa_encrypt_service = RSA(public_rsa_key_pair)
encoded_password = Encode2int(des_pwd)
encrypted_password = rsa_encrypt_service.Encrypt(encoded_password)
encrypted_des_pwd_chr = Decode2chr(encrypted_password)
with open('outbox/encrypted_pwd_des.txt', 'w') as encrypted_des_pwd_container:
encrypted_des_pwd_container.write(str(encrypted_des_pwd_chr))
print("DES password has been encrypted.") - 对确保信息完整性和一致性的散列值用发送方的非对称加密私钥进行加密作为“签名”,使发送方无法否认文件由他发送。
1
2
3
4
5
6
7
8
9
10
11
12
13
14def signature():
with open('sandbox_sender/private_key_sender.txt', 'r') as private_key_container:
private_key_pair_string = private_key_container.readline()
private_key_pair_string2pair_step_1 = private_key_pair_string.split(', ')
private_key_pair_string2pair_step_2_a = private_key_pair_string2pair_step_1[0].removeprefix('(')
private_key_pair_string2pair_step_2_b = private_key_pair_string2pair_step_1[1].removesuffix(')')
private_rsa_key_pair = int(private_key_pair_string2pair_step_2_a), int(private_key_pair_string2pair_step_2_b)
rsa_encrypt_service = RSA(private_rsa_key_pair)
encoded_hash = Encode2int(hash_abstract())
encrypted_hash = rsa_encrypt_service.Encrypt(encoded_hash)
encrypted_hash_chr = Decode2chr(encrypted_hash)
with open('outbox/encrypted_hash.txt', 'w') as hash_container_to_send:
hash_container_to_send.write(str(encrypted_hash_chr))
print("Hash has been signed (encrypted).")
因此,发送方需要发送的文件显然是加密过后的信息encrypted_msg.txt、加密过后的对称密码encrypted_pwd_des.txt和加密过后的散列值encrypted_hash.txt三个。
接收方
根据“发送方”章节中所提到的发送文件清单,接收方应当对这些文件有针对性地进行解密。不难得到他的任务如下:
1 | message_decrypt() |
- 使用自己的非对称加密私钥对
encrypted_pwd_des.txt进行解密,得到对称加密密码,随后凭此密码对encrypted_msg.txt进行解密,得到decrypted_msg.txt;1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32def des_pwd_decrypt():
with open('sent/encrypted_pwd_des.txt', 'r') as des_pwd_container:
des_pwd_encrypted = des_pwd_container.readline()
with open('sandbox_receiver/private_key_receiver.txt', 'r') as prv_key_radio:
private_key_pair_string = prv_key_radio.readline()
private_key_pair_string2pair_step_1 = private_key_pair_string.split(', ')
private_key_pair_string2pair_step_2_a = private_key_pair_string2pair_step_1[0].removeprefix('(')
private_key_pair_string2pair_step_2_b = private_key_pair_string2pair_step_1[1].removesuffix(')')
private_key_pair = int(private_key_pair_string2pair_step_2_a), int(private_key_pair_string2pair_step_2_b)
## print(public_key_pair_string2pair_step_2_a)
## print(public_key_pair_string2pair_step_2_b)
rsa_decrypt_service = RSA(private_key_pair)
encoded_encrypted_des_pwd = Encode2int(des_pwd_encrypted)
decrypted_encoded_des_pwd = rsa_decrypt_service.Decrypt(encoded_encrypted_des_pwd)
return str(Decode2chr(decrypted_encoded_des_pwd))
## The function to decrypt the message basing on the symmetric password decrypted (finished May 31 12:13 a.m.)
def message_decrypt():
decrypted_lines = ""
with open('sandbox_sender/desPassword.txt', 'r') as des_password_gotcha:
des_pwd = des_pwd_decrypt()
with open('sent/encrypted_msg.txt', 'r') as encrypted_message_container:
encrypted_message = encrypted_message_container.readline()
for i in range(int(len(encrypted_message) / 8)):
newTempText = [encrypted_message[j] for j in range(i * 8, i * 8 + 8)]
decrypted_lines = "".join([decrypted_lines, DES(newTempText, des_pwd, 1)])
## print(decrypted_lines)
with open('inbox/decrypted_msg.txt', 'w') as container_of_decrypted_contents:
container_of_decrypted_contents.write(decrypted_lines)
print("Message Decrypted.") - 使用发送方的非对称加密公钥对
encrypted_hash.txt进行解密,得到明文decrypted_hash.txt。随后自己再生成一次解密后的信息和密码对应的散列值,与decrypted_hash.txt进行比较;如果相同则代表信息在传输途中未被修改。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42def hash_decrypt():
with open('sent/encrypted_hash.txt', 'r') as hash_receipt:
encrypted_hash = hash_receipt.readline()
with open('public_key_sender.txt', 'r') as public_key_sender:
public_key_sender_string = public_key_sender.readline()
public_key_pair_string2pair_step_1 = public_key_sender_string.split(', ')
public_key_pair_string2pair_step_2_a = public_key_pair_string2pair_step_1[0].removeprefix('(')
public_key_pair_string2pair_step_2_b = public_key_pair_string2pair_step_1[1].removesuffix(')')
public_rsa_key_pair = int(public_key_pair_string2pair_step_2_a), int(public_key_pair_string2pair_step_2_b)
rsa_decrypt_service = RSA(public_rsa_key_pair)
encoded_hash = Encode2int(encrypted_hash)
encrypted_hash = rsa_decrypt_service.Decrypt(encoded_hash)
encrypted_hash_chr = Decode2chr(encrypted_hash)
with open('inbox/hash_decrypted.txt', 'w') as decrypted_hash:
decrypted_hash.write(str(encrypted_hash_chr))
print("Hash Decrypted.")
def hash_check():
with open('inbox/hash_decrypted.txt', 'r') as hash_decrypted:
hash_received = hash_decrypted.readline()
hash_received_list = hash_received.split(" ")
hash_received_1 = hash_received_list[0]
hash_received_2 = hash_received_list[1]
with open('sent/encrypted_msg.txt', 'r') as sample:
message = sample.read()
with open('sent/encrypted_pwd_des.txt', 'r') as encrypted_pwd:
password = encrypted_pwd.readline()
message_hash = MD5(message)
message_hash.fill_text()
message_hash_str = message_hash.group_processing()
if hash_received_1 != message_hash_str:
print(message_hash_str)
print("FATAL: Message has been modified half way.")
password_hash = MD5(password)
password_hash.fill_text()
password_hash_str = password_hash.group_processing()
if hash_received_2 != password_hash_str:
print("FATAL: Symmetric password has been modified half way.")
if hash_received_1 == message_hash_str and hash_received_2 == password_hash_str:
print("Message not vandalized. Transmit success.")
操作记录
根据上述运行一系列程序。首先运行的是initialization.py文件,对整个实验环境进行初始化。初始化完成后的输出结果和文件架构如下图所示;可以看到,目前的文件树只有sandbox_sender中有文件。这两个文件分别是待处理和发送的信息和对称加密密码。
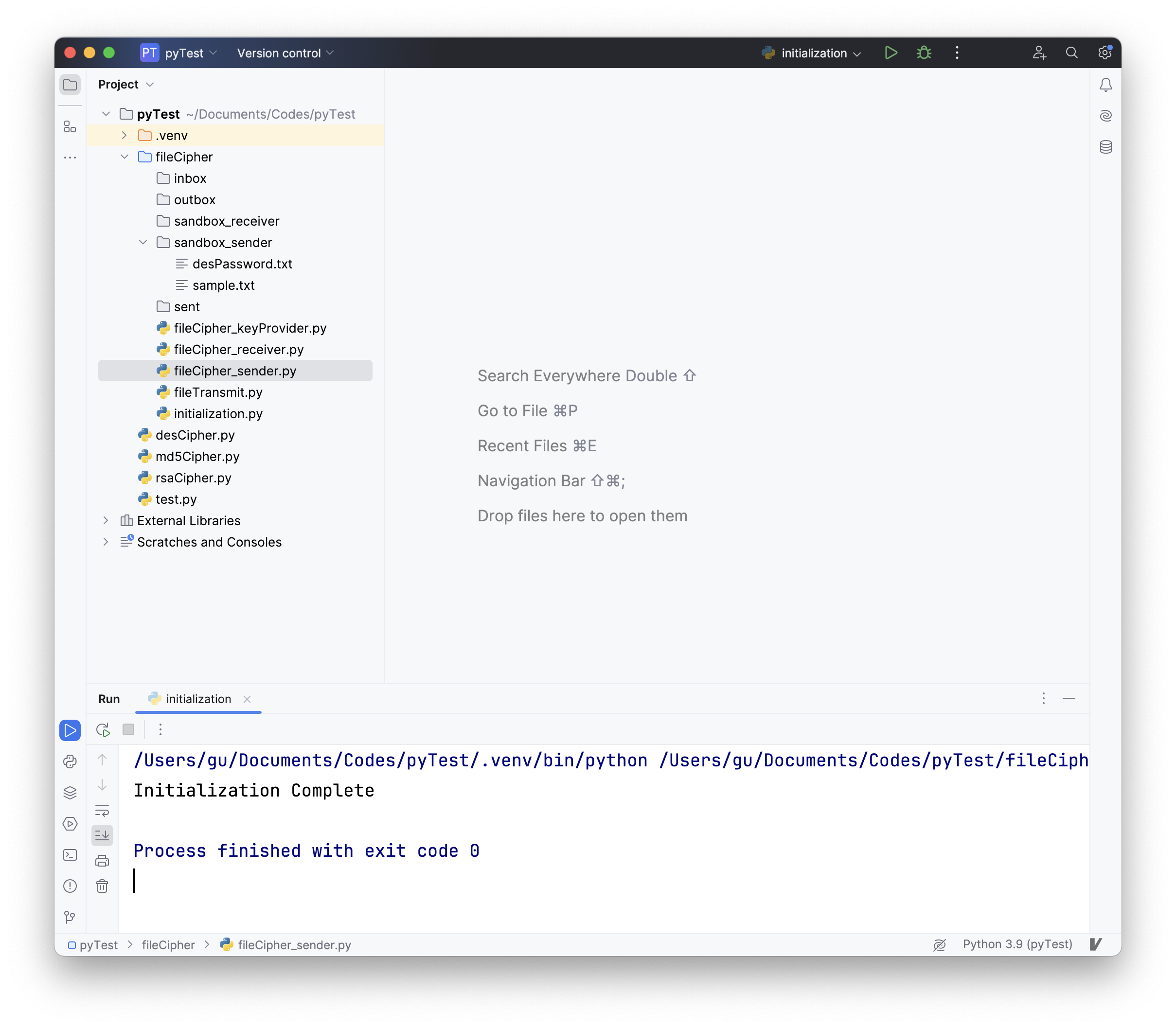
随后运行fileCipher_keyProvider.py。运行后的结果如图所示;此时该程式通过随机生成的质数197和239产生了发送方的非对称加密公私钥,并将前者放置在公共空间,将后者放置在sandbox_sender中;类似地,随机生成的质数157和239产生了接收方的非对称加密公私钥,并将前者放置在公共空间,将后者放置在sandbox_receiver中。
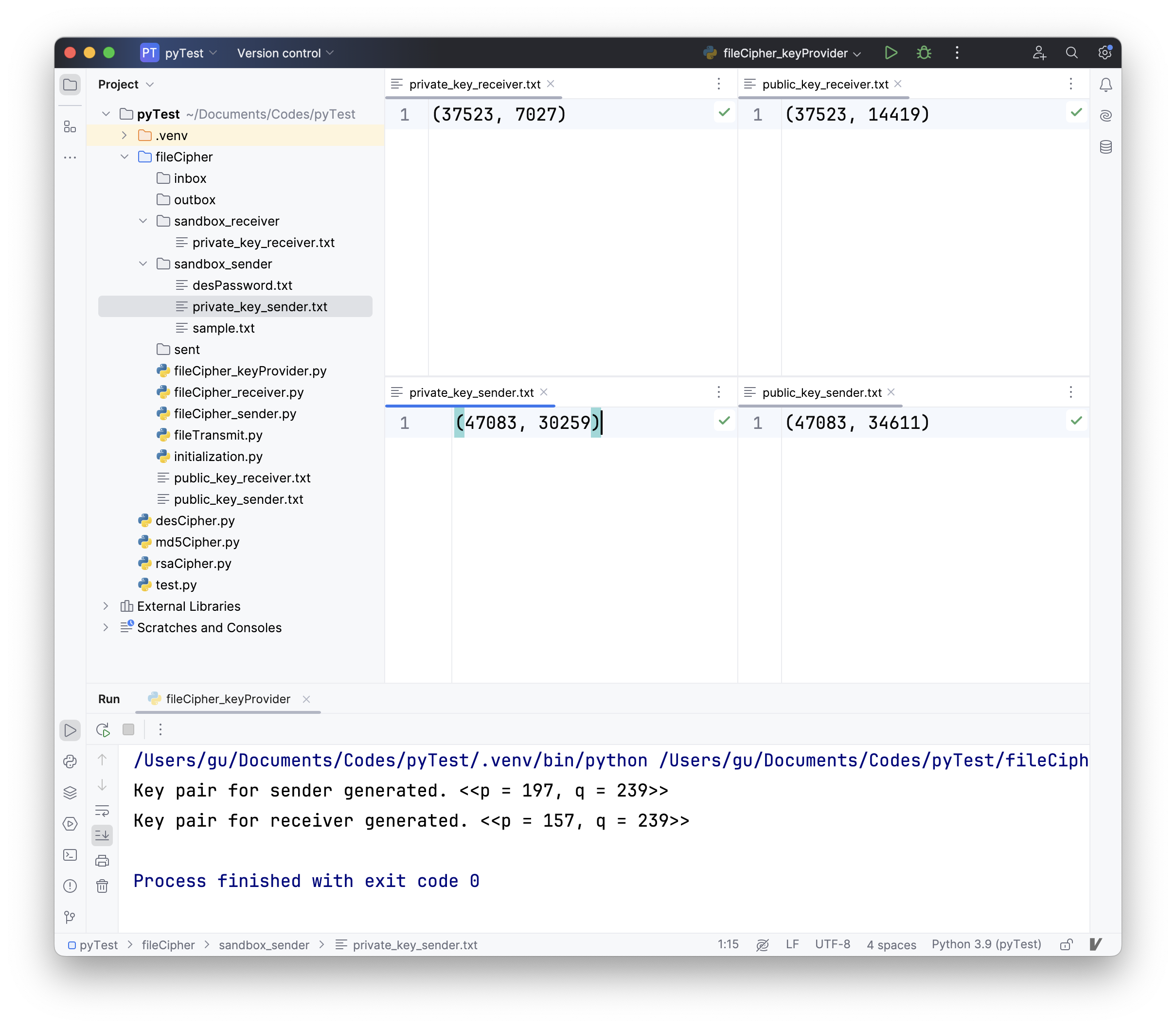
此时运行fileCipher_sender.py。运行后的结果如图所示;此时文件树已经在outbox中出现了信息、对称密码和散列值加密后的文件。
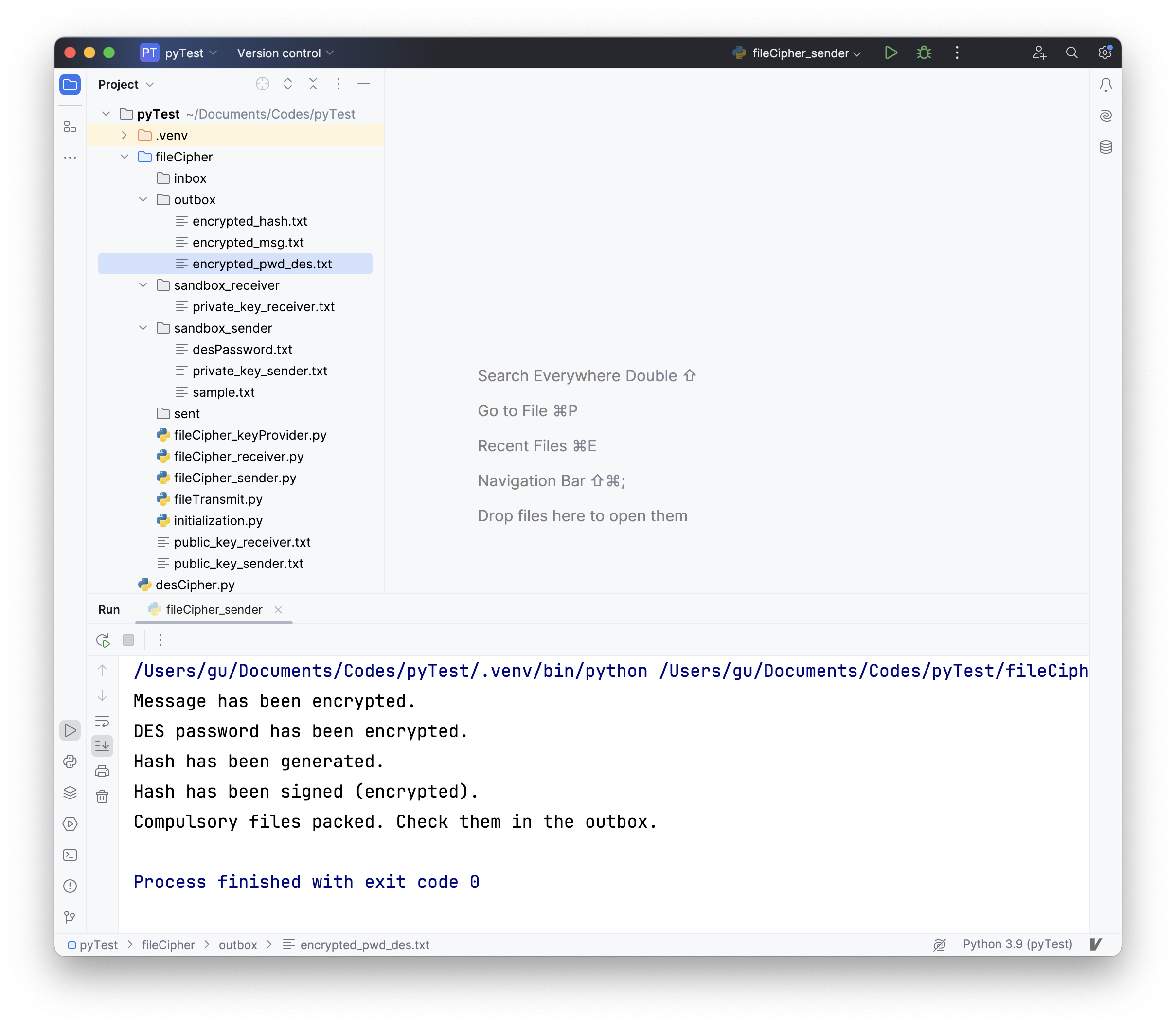
随后运行fileTransmit.py。运行后,outbox中的文件已经全部转移至sent。
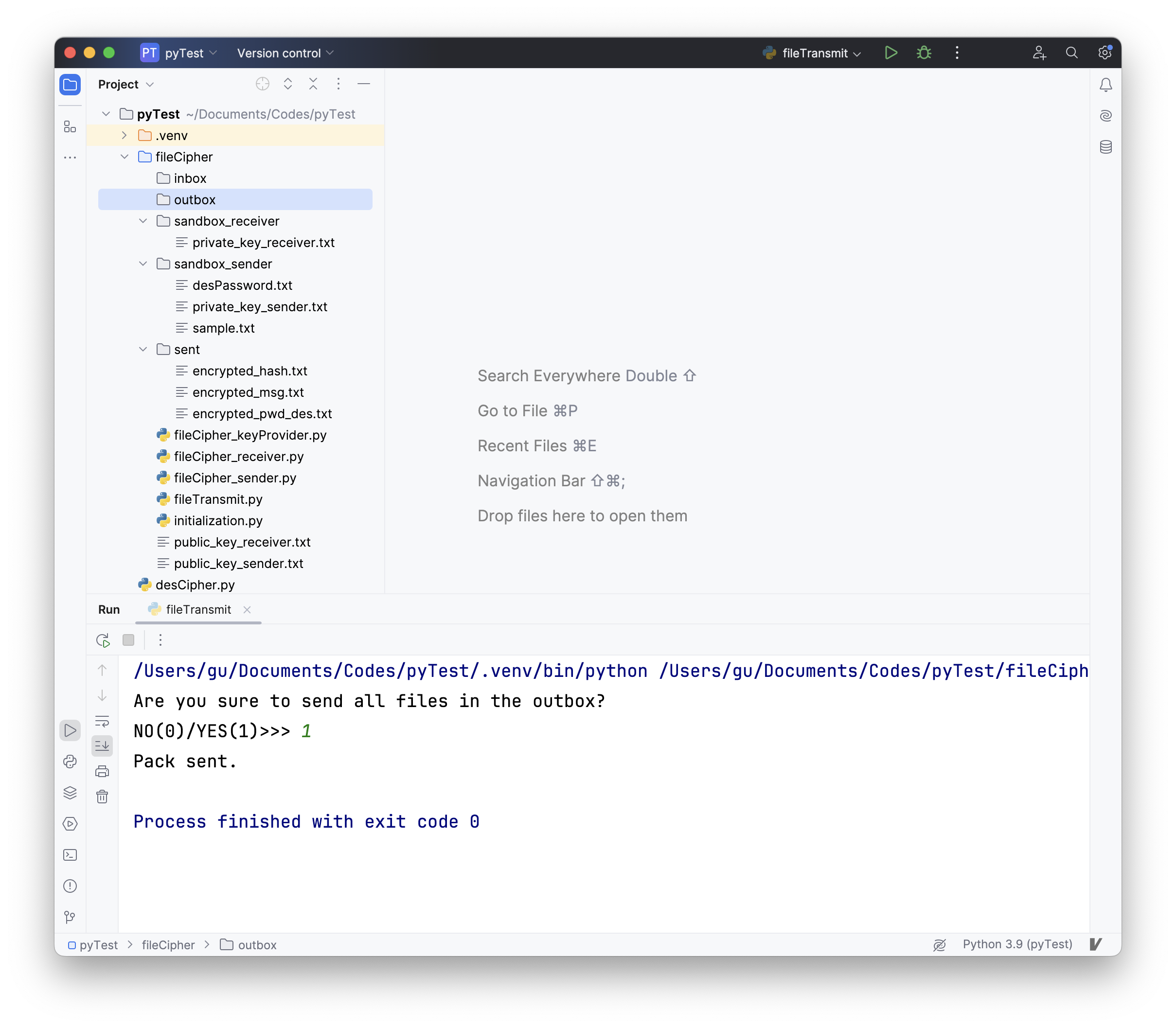
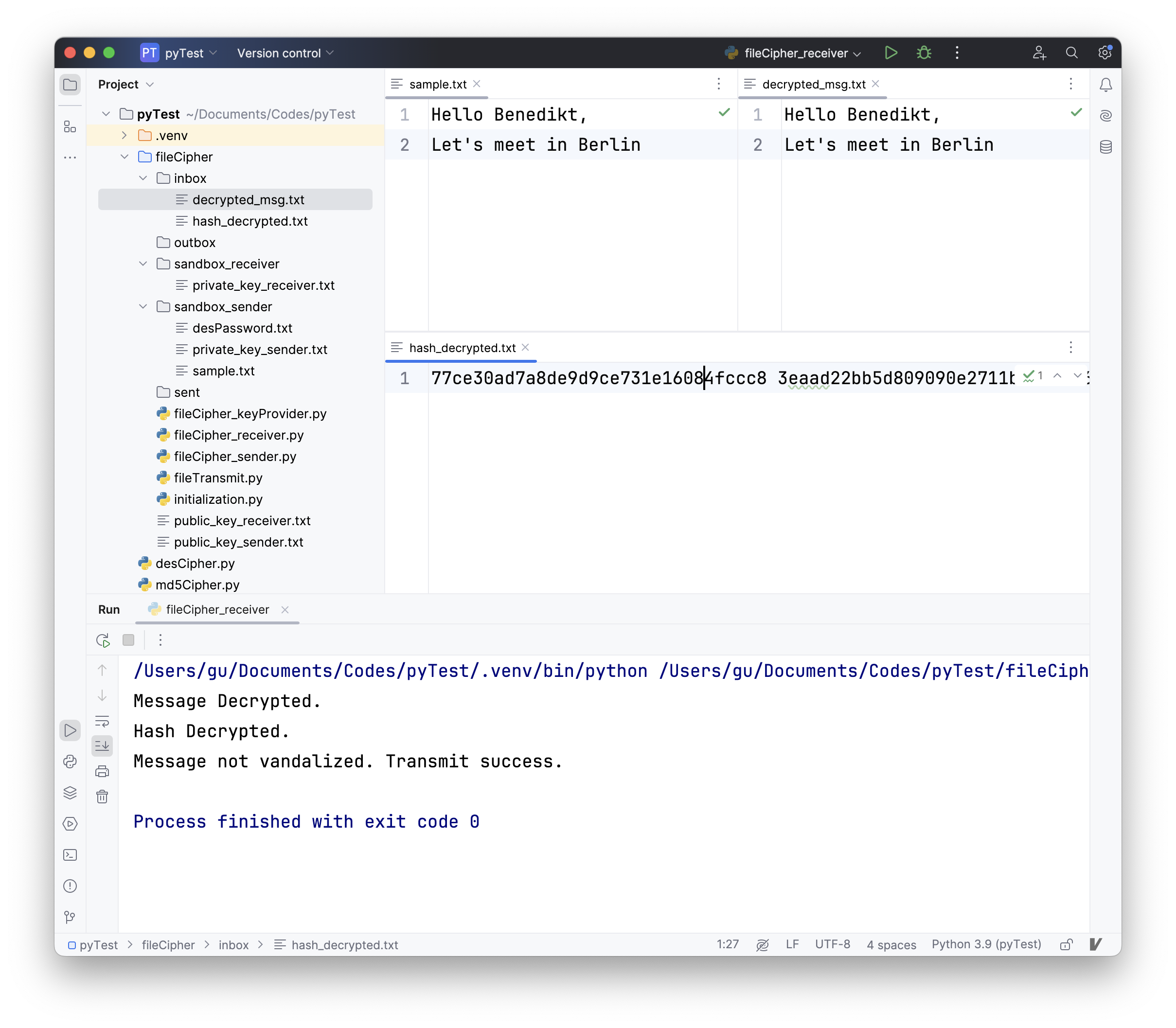
之后运行fileCipher_receiver.py。运行后,在inbox中得到信息明文和散列值。将信息明文decrypted_msg.txt与原信息sample.txt对比,发现文本内容一致;程式将解密后的散列值文件decrypted_hash.txt中的两段散列值分别与根据解密所得信息和对称加密密码重新生成的散列值进行比较,发现两散列值均一致,故输出信息未被损坏(“Message not vandalized”),进而得到传输成功的结论。
实验心得
实验过程中因为使用python,故不得不使用该语言的文件有关指令。在编写过程中进行调试时发现虽然python可以创建文件但是不能创建文件夹,因此为initialization.py额外增加了确认路径是否存在的操作。
本次实验虽然只进行了两个午后,但加深了我对密码学中比较具有代表性的这些典型加密方式对理解。不难看出,密码之所以“密”,恰因为每时每刻都有机制在进行更新;通过多种加密方式混合使用,可以很大程度上解决并不知道收发信双方约定加/解密顺序的情况下成功破译的潜在隐患。文件加密传输是密码学综合应用的集大成之作;在我们针对此实验集中精力于收发信双方的同时,作为密钥分发者的管理员也起着非常重要的作用。如果分发密钥者没有妥善保管好双方的私钥,纵使收发双方妥善保管了依然存在传输的信息被截获或被篡改的可能。只有整个文件加密传输过程中任何一个节点都能够保证符合流程规定,这个传输的过程才可以确定是安全的。






